Denoising Images with Autoencoders based on Convolutional Neural Networks¶

Version 1.1

This notebook is part of the book Applied Deep Learning: a case based approach, 2nd edition from APRESS by U. Michelucci and M. Sperti.

The purpose of this notebook is to give an example of Autoencoders implemented with convolutional neural networks applied to denoise images. The example dataset is taken from the real world.

Notebook Learning Goals¶

At the end of the notebook you will be able to implement yourself an autoencoder to be applied in a denoising problem (with convolutional networks). It is very instructive to compare this notebook with Denoising_autoencoders_with_FFNN.ipynb since they both solve the same problem, but with a different autoencoder architecture.

Libraries and Dataset Import¶

This section contains the necessary libraries (such as tensorflow or pandas) you need to import to run the notebook.

# general libraries
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from random import *

# tensorflow libraries
import tensorflow.keras as keras
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D, Conv2DTranspose
from tensorflow.keras.constraints import max_norm
from tensorflow.keras import backend as K
from keras.utils.vis_utils import plot_model

MNIST Dataset¶

For this notebook we will use the MNIST Dataset. You can check the dataset with the previous link. It can be easily imported using Keras. Below you can see how easy it is to download it using tensorflow.keras.datasets.

# Load MNIST dataset
(input_train, target_train), (input_test, target_test) = mnist.load_data()

# Reshape data based on channels first / channels last strategy.
# This is dependent on whether you use TF, Theano or CNTK as backend.
# Source: https://github.com/keras-team/keras/blob/master/examples/mnist_cnn.py

img_width, img_height = 28, 28

if K.image_data_format() == 'channels_first':
    input_train = input_train.reshape(input_train.shape[0], 1, img_width, img_height)
    input_test = input_test.reshape(input_test.shape[0], 1, img_width, img_height)
    input_shape = (1, img_width, img_height)
else:
    input_train = input_train.reshape(input_train.shape[0], img_width, img_height, 1)
    input_test = input_test.reshape(input_test.shape[0], img_width, img_height, 1)
    input_shape = (img_width, img_height, 1)

As usual we will do the typical normalisation of the datasets as you can see below. At this point in the book you should be able to understand the code below easily.

# Parse numbers as floats
input_train = input_train.astype('float32')
input_test = input_test.astype('float32')

# Normalize data
input_train = input_train / 255
input_test = input_test / 255

Let’s plot an image example for each possible class (i.e. digits from 0 to 9).

def get_random_element_with_label (data, lbls, lbl):
  """Returns one numpy array (one column) with an example of a choosen label."""
  
  tmp = lbls == lbl
  subset = data[tmp.flatten(), :]
  return subset[randint(0, subset.shape[0]), :]

# The following line is needed to reshape the training dataset 
# (to plot some image examples)
input_example = input_train.reshape(60000, 784)

# The following code create a numpy array where in column 0 you will find 
# an example of label 0, in column 1 of label 1 and so on.
labels_overview = np.empty([784, 10])
for i in range (0, 10):
    col = get_random_element_with_label(input_example, target_train, i)
    labels_overview[:,i] = col

f = plt.figure(figsize = (15, 15))
count = 1
for i in range(0, 10):
  plt.gray()
  plt.subplot(5, 2, count)
  count = count + 1
  plt.subplots_adjust(hspace = 0.5)
  plt.title('Digit: ' + str(i))
  some_digit_image = labels_overview[:, i]
  plt.imshow(some_digit_image.reshape(28, 28))
  plt.axis('off')
  pass

../_images/Denoising_autoencoders_with_CNN_18_0.png

Adding Noise to the Dataset¶

We know add a source of noise to the MNIST images (by means of np.random.normal function), since our objective will be to remove the same noise from them.

noise_factor = 0.55
pure = input_train
pure_test = input_test
noise = np.random.normal(0, 1, pure.shape)
noise_test = np.random.normal(0, 1, pure_test.shape)
noisy_input = pure + noise_factor * noise
noisy_input_test = pure_test + noise_factor * noise_test

Now, let’s plot some examples of images corrupted by noise (one for each class, as in the figure above).

# The following line is needed to reshape the training dataset 
# (to plot some image examples)
input_example_noise = noisy_input.reshape(60000, 784)

# The following code create a numpy array where in column 0 you will find 
# an example of label 0, in column 1 of label 1 and so on.
labels_overview = np.empty([784, 10])
for i in range (0, 10):
    col = get_random_element_with_label(input_example_noise, target_train, i)
    labels_overview[:,i] = col

f = plt.figure(figsize = (15, 15))
count = 1
for i in range(0, 10):
  plt.gray()
  plt.subplot(5, 2, count)
  count = count + 1
  plt.subplots_adjust(hspace = 0.5)
  plt.title('Digit: ' + str(i))
  some_digit_image = labels_overview[:, i]
  plt.imshow(some_digit_image.reshape(28, 28))
  plt.axis('off')
  pass

../_images/Denoising_autoencoders_with_CNN_25_0.png

Autoencoder with Convolutional Neural Networks¶

Now we need to create the keras models. An autoencoder is made of two main parts: an encoder and a decoder. The function below create_autoencoders() returns the model.

def create_autoencoders(max_norm_value = 2.0):
  # Create the model
  model = Sequential()
  model.add(Conv2D(64, kernel_size = (3, 3), kernel_constraint = max_norm(max_norm_value), activation = 'relu', kernel_initializer = 'he_uniform', input_shape = input_shape))
  model.add(Conv2D(32, kernel_size = (3, 3), kernel_constraint = max_norm(max_norm_value), activation = 'relu', kernel_initializer = 'he_uniform'))
  model.add(Conv2DTranspose(32, kernel_size = (3,3), kernel_constraint = max_norm(max_norm_value), activation = 'relu', kernel_initializer = 'he_uniform'))
  model.add(Conv2DTranspose(64, kernel_size = (3,3), kernel_constraint = max_norm(max_norm_value), activation = 'relu', kernel_initializer = 'he_uniform'))
  model.add(Conv2D(1, kernel_size = (3, 3), kernel_constraint = max_norm(max_norm_value), activation = 'sigmoid', padding = 'same'))
  return model

model = create_autoencoders()

plot_model(model, show_shapes = True)

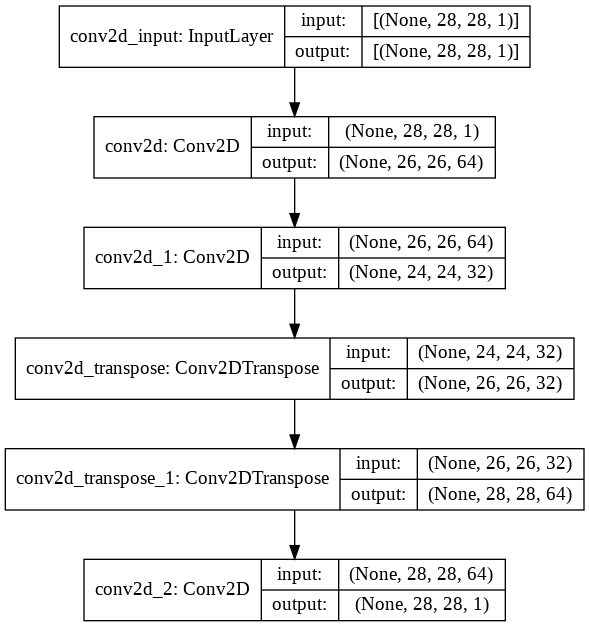
../_images/Denoising_autoencoders_with_CNN_30_0.png

As for any Keras model we need to compile the model and then fit it to the data. As you can see we don’t need any custom code to work with autoencoders. A simple model definition \(\rightarrow\) compile \(\rightarrow\) fit is enough.

# Model configuration
batch_size = 150
no_epochs = 30
validation_split = 0.2

# Compile and fit data
model.compile(optimizer = 'adam', loss = 'binary_crossentropy')
model.fit(noisy_input, pure,
          epochs = no_epochs,
          batch_size = batch_size,
          validation_split = validation_split)

Epoch 1/30
320/320 [==============================] - 39s 19ms/step - loss: 0.1923 - val_loss: 0.1077
Epoch 2/30
320/320 [==============================] - 6s 18ms/step - loss: 0.1061 - val_loss: 0.1042
Epoch 3/30
320/320 [==============================] - 6s 18ms/step - loss: 0.1027 - val_loss: 0.1020
Epoch 4/30
320/320 [==============================] - 6s 18ms/step - loss: 0.1013 - val_loss: 0.1010
Epoch 5/30
320/320 [==============================] - 6s 18ms/step - loss: 0.1003 - val_loss: 0.1004
Epoch 6/30
320/320 [==============================] - 6s 18ms/step - loss: 0.0996 - val_loss: 0.0996
Epoch 7/30
320/320 [==============================] - 6s 18ms/step - loss: 0.0993 - val_loss: 0.0992
Epoch 8/30
320/320 [==============================] - 6s 18ms/step - loss: 0.0987 - val_loss: 0.0990
Epoch 9/30
320/320 [==============================] - 6s 18ms/step - loss: 0.0983 - val_loss: 0.0987
Epoch 10/30
320/320 [==============================] - 6s 18ms/step - loss: 0.0982 - val_loss: 0.0986
Epoch 11/30
320/320 [==============================] - 6s 18ms/step - loss: 0.0978 - val_loss: 0.0982
Epoch 12/30
320/320 [==============================] - 6s 18ms/step - loss: 0.0975 - val_loss: 0.0982
Epoch 13/30
320/320 [==============================] - 6s 18ms/step - loss: 0.0971 - val_loss: 0.0981
Epoch 14/30
320/320 [==============================] - 6s 18ms/step - loss: 0.0974 - val_loss: 0.0977
Epoch 15/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0971 - val_loss: 0.0978
Epoch 16/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0970 - val_loss: 0.0976
Epoch 17/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0970 - val_loss: 0.0976
Epoch 18/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0967 - val_loss: 0.0975
Epoch 19/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0968 - val_loss: 0.0973
Epoch 20/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0968 - val_loss: 0.0972
Epoch 21/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0965 - val_loss: 0.0974
Epoch 22/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0965 - val_loss: 0.0975
Epoch 23/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0962 - val_loss: 0.0972
Epoch 24/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0966 - val_loss: 0.0971
Epoch 25/30
320/320 [==============================] - 6s 18ms/step - loss: 0.0963 - val_loss: 0.0971
Epoch 26/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0962 - val_loss: 0.0970
Epoch 27/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0960 - val_loss: 0.0969
Epoch 28/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0961 - val_loss: 0.0975
Epoch 29/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0959 - val_loss: 0.0969
Epoch 30/30
320/320 [==============================] - 6s 19ms/step - loss: 0.0959 - val_loss: 0.0970

<tensorflow.python.keras.callbacks.History at 0x7f93d6752550>

Examples of Denoised Images¶

Now we plot some examples of denoised images, comparing them with the original pure images, to see how well the built autoencoder behaves.

# Generate denoised images
number_of_visualizations = 6
samples = noisy_input_test[:number_of_visualizations]
targets = target_test[:number_of_visualizations]
denoised_images = model.predict(samples)

# Plot denoised images
for i in range(0, number_of_visualizations):
  plt.gray()
  # Get the sample and the reconstruction
  noisy_image = noisy_input_test[i][:, :, 0]
  pure_image  = pure_test[i][:, :, 0]
  denoised_image = denoised_images[i][:, :, 0]
  input_class = targets[i]
  # Matplotlib preparations
  fig, axes = plt.subplots(1, 3)
  fig.set_size_inches(12, 7)
  # Plot sample and reconstruction
  axes[0].imshow(noisy_image)
  axes[0].set_title('Noisy image', fontsize = 16)
  axes[0].get_xaxis().set_visible(False)
  axes[0].get_yaxis().set_visible(False)
  axes[1].imshow(pure_image)
  axes[1].set_title('Pure image', fontsize = 16)
  axes[1].get_xaxis().set_visible(False)
  axes[1].get_yaxis().set_visible(False)
  axes[2].imshow(denoised_image)
  axes[2].set_title('Denoised image', fontsize = 16)
  axes[2].get_xaxis().set_visible(False)
  axes[2].get_yaxis().set_visible(False)
  fig.suptitle(f'MNIST target = {input_class}')
  plt.show()

<Figure size 432x288 with 0 Axes>

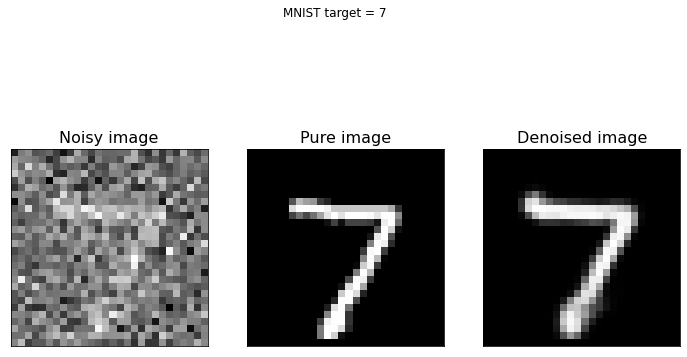
../_images/Denoising_autoencoders_with_CNN_37_1.png

<Figure size 432x288 with 0 Axes>

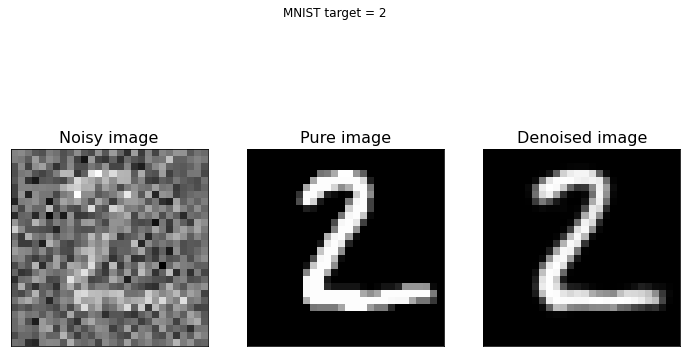
../_images/Denoising_autoencoders_with_CNN_37_3.png

<Figure size 432x288 with 0 Axes>

../_images/Denoising_autoencoders_with_CNN_37_5.png

<Figure size 432x288 with 0 Axes>

../_images/Denoising_autoencoders_with_CNN_37_7.png

<Figure size 432x288 with 0 Axes>

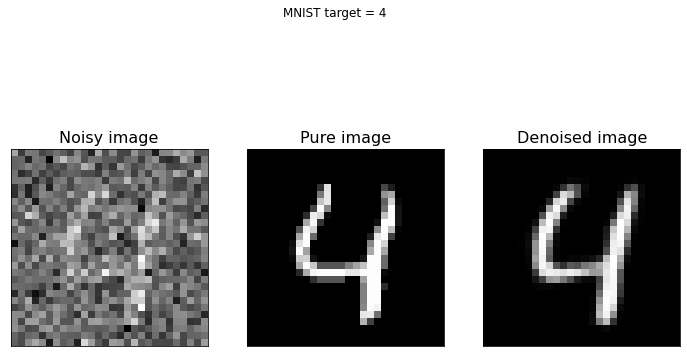
../_images/Denoising_autoencoders_with_CNN_37_9.png

<Figure size 432x288 with 0 Axes>

../_images/Denoising_autoencoders_with_CNN_37_11.png

As you can see from the above figure, the model we built can reconstruct the original version of noisy digit images. If you have new noisy images of the same type you can apply the model to them and de-noise the same images.

If you compare this last figure with the last figure of Denoising_autoencoders_with_FFNN.ipynb notebook, you can notice that CNNs are better suited to this kind of task. In fact, they are specifically designed for working with images, more than FFNNs.

Applied Deep Learning - 2nd Edition